math art by dan bach
this page is scrollable. click or tap the (+) button for more info on some images
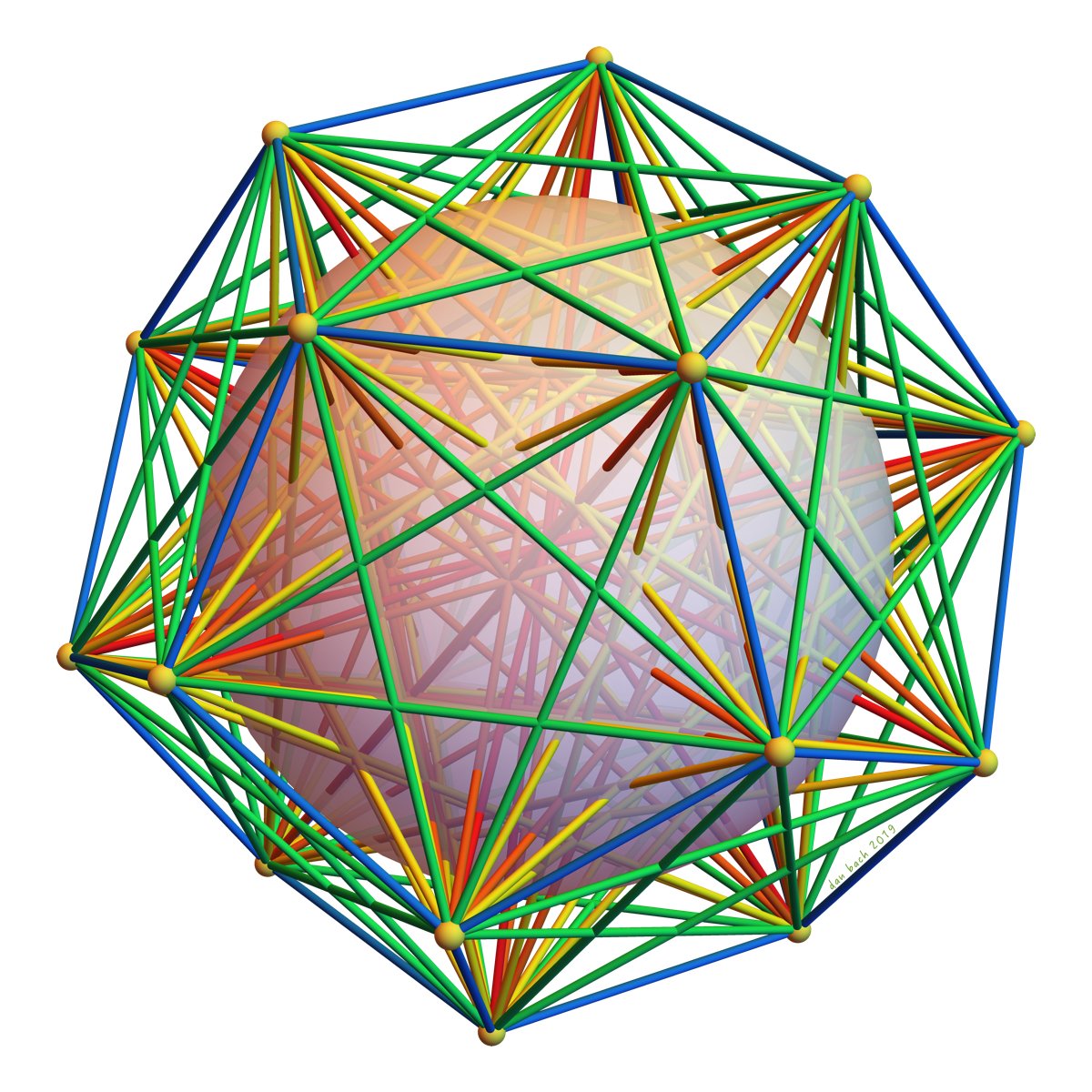
at a small hideaway in sonoma, california lives a metal sphere apparently about 7 feet in diameter, and hence about 22 feet around.
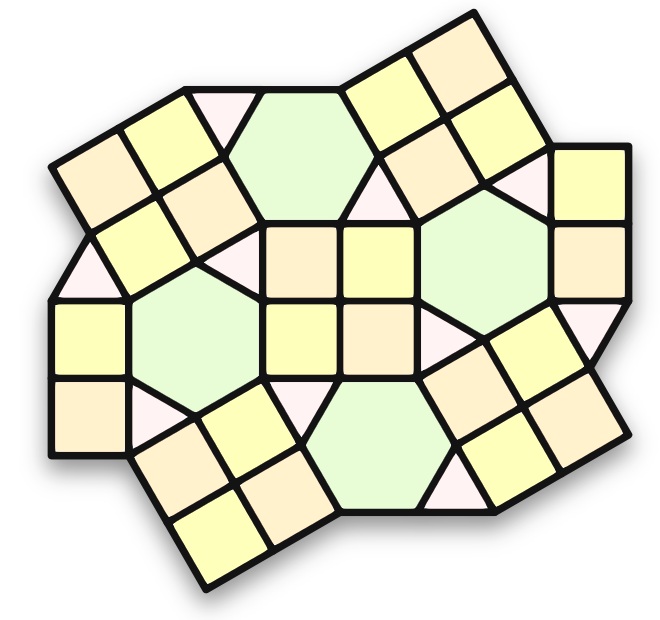
that's an interesting pattern on the surface. any guess as to how many little shapes cover the sphere? my hand fits through one of them. is it a polyhedron?
the basic saddle (x, y, z) = (cos(t), sin(t), cos(2t)) is adorned with hundreds of sine waves based on the tangent, normal, and binormal vectors. trig functions attached to the {T, N, B} frame tell the story here.
starting with the outer red curve (a slightly wiggly circle), the curves change color as they march inward toward the center of curvature at each point. the slight wobble is magnified, especially vertically, as the curves go from orange to blue-green. this object has become my go-to lo-go.
i dreamed up a twisty central curve and made mathematica draw the curves around it, with weird combinations of the T, N, B vectors doing the job. the spheres are sized to just touch the wires.
there are lots of circles in this picture, but NONE OF THEM touch any others! based on a 1983 article I rescued from an old pile of AmerMathMonthly, I told Mathematica to put circles on each spherical shell that avoid the intersection with the vertical red rings.
made in girih.app - this tiling of triangles, squares, and hexagons can be extended to fill the whole plane.
a 3D loopy curve is adorned with parallel normal curves and lots of binormal struts with a colored ball on the end of each one.
each spiraling spoke of length n has all of its divisors sitting on top of it. some n have lots of sitters, primes have just 1. there are 60 numbers in each revolution, 196 is the last n. what do you notice? can you see the primes? which n has the most divisors?
the 3d hilbert curve is the limit of square-cornered paths that increasingly fill up the unit cube. i told mathematica to replace the paths with spline curves. here we have hilbert splines 1, 2, and 3, joined by soap films between the 1-2 and the 2-3. the films then cast a translucent shadow on the beach.
A central loopy tube, defined by trig functions, is surrounded by a long green vine, which has sprouted a few hundred leaves. The tube is called a 3D lissajous figure, and it helps line up the leaves, which are flat cylinders. The shadow is fake, just the original image compressed and skewed for perspective.
The Platonic dodecahedron (blue) shows off its space diagonals of all possible lengths. The sphere barges in and obscures a lot of them, but you can imagine them fighting for space in the center of the picture.
The red saddle curve has a tangent direction, then a normal direction towards the center of curvature, and also a binormal direction perpendicular to the first two. Parallel curves in both directions give this object its depth, and a few Moiré patterns as well.
